מתמטיקה תיכונית/הנדסה אנליטית/חתכי חרוט

		הדף נמצא בשלבי עבודה: כדי למנוע התנגשויות עריכה ועבודה כפולה אתם מתבקשים שלא לערוך ערך זה בטרם תוסר הודעה זו, אלא אם כן תיאמתם זאת עם מניחי התבנית.
		אם הדף לא נערך במשך שבוע ניתן להסיר את התבנית ולערוך אותו, אך רצוי לתת קודם תזכורת בדף שיחת הכותבים.	שיחה

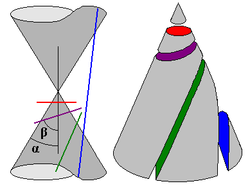
הצורות הגיאומטריות כחתכי חרוט

קובץ:Apollonios of Perga.jpeg

אפולוניוס, בסביבות 262 - 190 לפנה"ס

חתכי חרוט, הם הצורות הגיאומטריות הנוצרות ממישור החותך חרוט.

הצורות הגיאומטריות מעגל, אליפסה, פרבולה והיפרבולה, מוכרות בהגדרתם כמקום גיאומטרי המקיים תנאים מסוימים, או באמצעות תיאורם כמשוואה ממעלה שנייה. להלן תבוא הגדרה נוספת לתיאורם באמצעות מישור החותך חרוט. הראשון שחקר את חיתוכי החרוט הוא המתמטיקאי היווני אפולוניוס, בן המאה השניה לפני הספירה, בספרו "תורת החרוטים". אפולוניוס הראה שהצורות הגיאומטריות: מעגל, אליפסה, פרבולה והיפרבולה, יכולים להתקבל מחיתוך של אותו החרוט, רק בזווית שונה.

הגדרה מקדימה - "חרוט מעגלי"

לצורך פשטות העניין, נדגים את חיתוכי החרוט באמצעות חרוט עיגולי.

חרוט עיגולי מוגדר כ"שטח המרחבי הנוצר מישר הנע דרך מעגל קבוע, והעובר בנקודה O הנמצאת מעל מרכז המעגל". כמודגם באיור הבא:

הקו הנראה לאורכו של החרוט משמאל, הוא היישר העובר דרך המעגל (המתווה את בסיס החרוט) ובנקודה O אשר מעל מרכז המעגל (אשר בה קודקוד החרוט, ובאיור שלפנינו - נקודת החיבור בין שני קודקודי החרוט).

הקו שהוצג באיור, המחבר את קודקוד החרוט עם נקודה שעל מעגל הבסיס, מהווה קו אחד מתוך אינסוף קדים המחברים כל נקודה שעל המעגל עם הקודקוד (וממשיכים לעבר המעגל שבחרוט העליון). קווים אלו מכונים: קוי היוצר של החרוט.

ציר החרוט הוא הקו המחבר את הקודקוד עם מרכז המעגל שבבסיס (העליון והתחתון).

הקווים הירוקים - אלו הם קוי היוצר של החרוט, הקו הכחול הוא ציר החרוט. מעגל הבסיס הוא המעגל המותווה בבסיס החרוט.

הגדרת הצורות הגאומטריות לפי חיתוכי חרוט

בהתאם למושגים שנגדרו בפסקה הקודמת, נגדיר עתה את ארבע הצורות הגאומטריות, מעגל, אליפסה, פרבולה והיפרבולה, לפי חיתוכי החרוט.

• מישור החותך את החרוט במקביל למעגל הבסיס (ובמאונך לציר החרוט) - הוא מעגל.
• מישור החותך את החרוט שלא במקביל למעגל הבסיס, (אולם זווית הנטייה שלו פחותה מנטיית הקו היוצר של החרוט) - הוא אליפסה.
• מישור החותך את החרוט במקביל לקו היוצר של החרוט - הוא פרבולה.
• מישור החותך את החרוט בזווית הנטויה יותר מנטיית הקו היותר של החרוט (בתנאי שהוא לא חותך אותו לאורכו באמצעו, בנקודת חיבור הקודקודים) - הוא היפרבולה

ארבע הצורות הגיאומטריות המתקבלות ממישור החותך חרוט כפול. הימני: היפרבולה, האמצעי: למעלה - אליפסה, למטה - מעגל, השמאלי: פרבולה

נספח - ההגדרות השונות לצורות הגיאומטריות

הגדרה גיאומטרית

חתכי החרוט ניתנים להגדרה גם כמקומות הגאומטריים הבאים:

• אוסף הנקודות הנמצאות במרחק קבוע מנקודה נתונה הוא מעגל.
• אוסף הנקודות שסכום מרחקיהן משתי נקודות נתונות הוא קבוע, הוא אליפסה.
• אוסף הנקודות שמרחקן מנקודה נתונה שווה למרחקן מישר נתון הוא פרבולה.
• אוסף הנקודות שהפרש המרחקים שלהן משתי נקודות נתונות קבוע הוא היפרבולה.

הגדרה אלגברית

חתכי החרוט ניתנים להגדרה גם כמשוואה ממעלה שנייה:

• מעגל מיוצג כאוסף המקומות הגיאומטריים $\ (x,y)$ המקיימים את המשוואה הבאה $\!\,(x-x_{0})^{2}+(y-y_{0})^{2}=R^{2}$
  :כאשר $\!\,(x_{0},y_{0})$ היא מרכז המעגל ו $\ R$ הוא רדיוס המעגל.
• אליפסה קנונית מיוצגת כאוסף המקומות הגיאומטריים $\ (x,y)$ המקיימים את המשוואה הבאה ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$
  :כאשר $\ A$ מייצגת את שיעור מחצית הצור הארוך של האליפסה, ו-$\ B$ מייצגת את שיעור מחצית הציר הקצר של האליפסה.
  :(הגדרה אחרת ל-$\ B$: $\ B$ מייצגת את שיעור ההפרשים $\ (a^{2}-F^{2})$. כאשר $\ F$ מייצגת את הנקודה הקבועה אשר ממנה ומהנקודה הסימטרית לה נמדדים המרחקים לכל נקודה שעל האליפסה).
• היפרבולה קנונית מיוצגת כאוסף המקומות הגיאומטריים $\ (x,y)$ המקיימים את המשוואה הבאה: ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

ראו גם

ערך בוויקיפדיה: חתכי חרוט

תמונות ומדיה בוויקישיתוף: חתכי חרוט

• עמוס אלטשולר, חתכי החרוט בגישה סינתטית, (הוכחות קלאסיות לעקומים המתקבלים על ידי חתכי החרוט), על"ה - עלון למורי המתמטיקה, גליון 9, ספטמבר 1991.
• ד"ר חמוטל דוד, ערכת לימוד על חתכי חרוט,