תורת החישוביות/כריעות שפות/שפות שאינן כריעות/ארגז חול
בחלקים הקודמים ראינו מספר קבוצות של שפות:
R,
RE,
coRE,
וכמובן, קבוצת העל
.
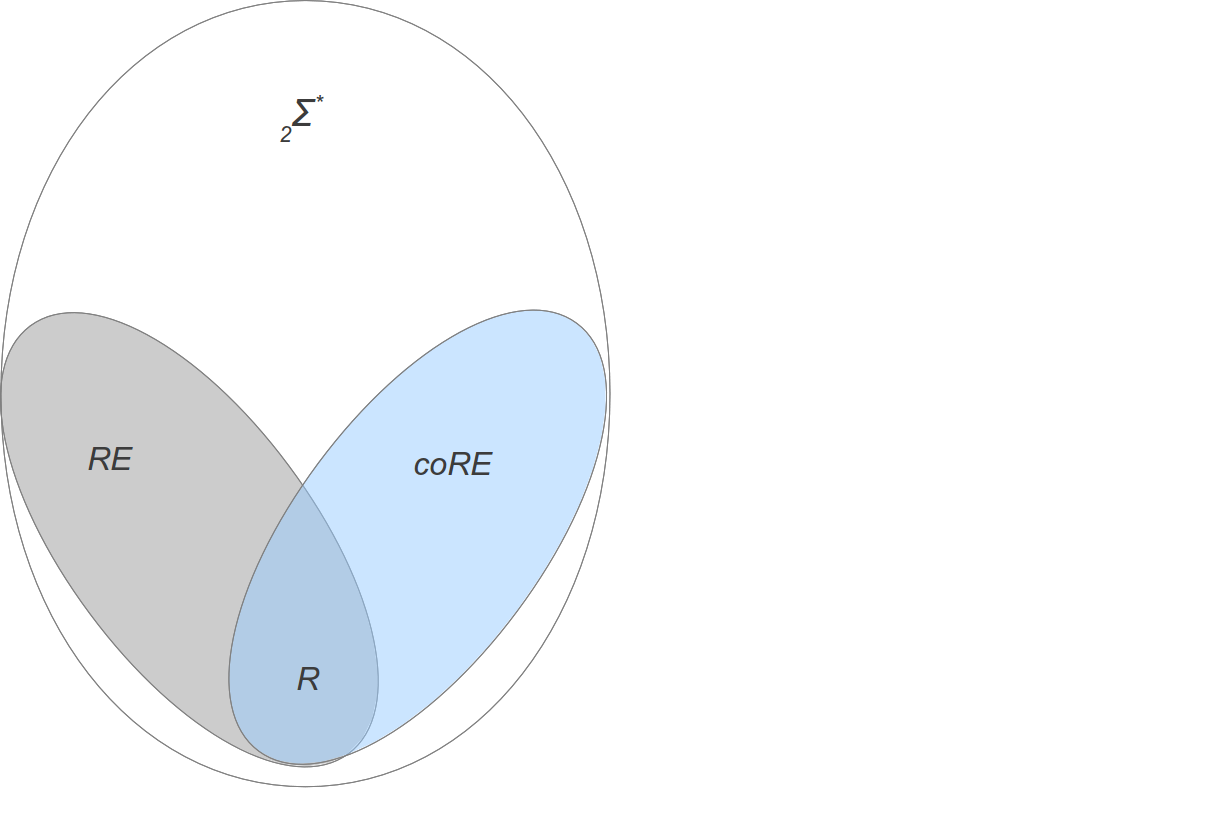
בחלק זה נראה ש"תמונת העולם" נראית כבתרשים הבא.
כלומר,
- ישנן שפות ב
- ישנן שפות ב
- הקבוצה R הנה חתוך RE וcoRE (את זאת כבר ראינו).
הקבוצה איננה ריקה
עריכה|
שקלו לדלג על נושא זה חלק זה משתמש בעוצמות קבוצות. אפשר להבין את שאר החומר גם ללא חלק זה. |
משיקולי מניה אפשר לראות שבהכרח יש שפות ב .
ראשית נראה שיש יותר שפות ממחרוזות.
|
טענה: יש יותר שפות ממחרוזות (או: קבוצת כלל המחרוזות מעל היא בת-מניה, ואילו קבוצת כל השפות אינה בת-מניה). |
הוכחה: אפשר לראות שקבוצת השפות הנה קבוצת תתי הקבוצות של
,
שהיא כידוע .
לחלופין, אפשר להוכיח ישירות שקבוצת השפות אינה בת-מניה באופן דומה לאלכסון של קנטור.
נסמן את קבוצת כל המילים מעל ב־x ונכתוב אותן לפי הסדר הלקסיקוגרפי:
נניח בשלילה שקבוצת כל השפות היא בת מנייה, ונסמנה ב־A.
נגדיר את השפה D:
כלומר, אם המילה נמצאת ב־ אז היא לא ב־D. אך אם אינה ב־ אז היא כן תהיה ב־D. ניתן לרשום זאת בצורת טבלה בה כל שורה היא אחת השפות וכל עמודה היא אחת המילים נסמן 1 אם ו־0 אחרת.
כעת נוכיח שהשפה D אינה אחת מהשפות . נביט על האלכסון. אם עבור מילה מסויימת הרי שהיא אינה ב־ , ולכן . למעשה – האלכסון מגדיר את .
בעזרת הטענה הקודמת, אפשר לראות שבהכרח ישנן שפות ב
הוכחה: ההוכחה היא משיקולי ספירה.
- מספר השפות בRE הוא לכל היותר מספר מ״ט השונות, כי כל מ״ט מגדירה שפה, ואם השפה ב־RE אז יש מ״ט שמקבלת כל מילה בה. מאידך, כמות מ״ט הקיימות הוא לכל היותר כמות המחרוזות מעל האלפבית הבינארי, מכיוון שכל מ״ט ניתנת לקידוד למחרוזת בינארית.
כפי שראינו בטענה הקודמת, יש יותר שפות ממחרוזות, ולכן יש יותר שפות מאשר השפות בRE.
הקבוצה איננה ריקה
עריכהבחלק קודם כבר ראינו מספר דוגמאות לשפות בRE: השפה האוניברסלית, שפת האלכסון, ובעיית העצירה. כעת נראה כי שפות אלו הן ב .
אי-כריעות בעיית העצירה
עריכהנניח, על דרך השלילה, שקיימת מ"ט כריעה, העונה על השאלה האם מ"ט M עוצרת על קלט x. נקרא למכונה זו H. כעת נבנה את המכונה באופן הבא:
- בהנתן קידוד מ"ט M, המכונה קודם תריץ את , (נזכור שתמיד חלק זה עוצר, שכן הנחתנו בשלילה היא שהבעיה כריעה, וH מימוש שלה).
- אם התשובה חיובית, אז תכנס ללולאה אינסופית. אחרת, היא תעצור.
כעת נקבל מצב אבסורד לגבי הריצה :
- אם היא עוצרת, אז בהכרח מחזירה תשובה שלילת (מפני שהיא השלב הראשון בריצת שכתוצאתו הוחלט לעצור). אבל לפי ההגדרה, משמעות תשובה שלילית זו היא ש איננה עוצרת, ולכן יש סתירה.
- אם היא איננה עוצרת, אז בהכרח מחזירה תשובה חיובית (שוב, מפני שהיא השלב הראשון בריצת שכתוצאתו הוחלט להכנס ללולאה אינסופית). אבל לפי ההגדרה, משמעות תשובה חיובית זאת היא ש עוצרת, ולכן שוב יש סתירה.
אי-כריעות משלימת שפת האלכסון
עריכהנתבונן בשפה המשלימה לשפת האלכסון, כלומר
.
|
טענה:
|
הוכחה: נניח בשלילה שאכן , ולכן קיימת מ״ט שמכריעה את . האם המכונה תקבל את המחרוזת ?
- אם אזי מהגדרת השפה נובע כי . במילים אחרות, אם מריצים את על המחרוזת , המכונה לא תקבל את הקלט, ובפרט היא תדחה אותו (כי היא מכונה מכריעה). אבל, זו סתירה, כי הנחנו ש־ , כלומר, הקלט בשפה ו־ צריכה לקבל אותו מכיוון שהיא מכריעה את השפה.
- לחלופין, אם מניחים כי המחרוזת אינה בשפה, , אזי המכונה צריכה לדחות את הקלט . מכאן ש־ אינה מקבלת את המחרוזת של עצמה, ולכן היא שייכת ל־ , או באופן יותר מדוייק, הקידוד שלה נמצא בשפה זו, וזו סתירה להנחה.
אי-כריעות שפות נוספות דרך תכונות בסיסיות של רדוקציות ומשפטי רדוקציות
עריכהבחלק זה נשתמש בתכונות בסיסיות של רדוקציות ומשפטי רדוקציה כדי להראות שמספר שפות אינן כריעות.
|
טענה: השפה האלכסונית אינה כריעה, . |
הוכחה: נשים לב ש־R סגורה למשלים. לפיכך, מכיוון ש־ , כך גם השפה המשלימה.
|
טענה:
|
הוכחה: ראינו בפרק רדוקציה שמתקיים ולפי משפט הרדוקציה – ההפכי נובעת המסקנה.
|
טענה:
|
הוכחה: ראינו בפרק רדוקציה שמתקיים ולפי משפט הרדוקציה – ההפכי נובעת המסקנה.
| - | ארגז חול | - |